Conduite distributrice

Relation analytique pour le calcul direct des pertes de charge en conduite distribuant un débit de façon homogène établi à partir de la formule de Blasius.

Hypothèses

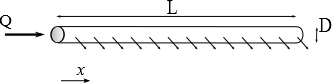
On suppose une conduite de longueur \(L\), diamètre intérieur \(D\), avec un débit en tête \(Q\). On calcule la perte de charge \(\Delta H\) entre les 2 extrémités de la conduite. Dans une section de débit \(q\) constant, on évalue le coefficient de frottement avec la formule de Blasius, valide pour des nombres de Reynolds modérés pour des parois lisses:

\[\lambda \simeq a Re^{-0.25}\]

Développement analytique

On note \(x\) la position depuis l'aval de la conduite. Le débit est supposé varier linéairement avec \(x\), et s'écrit alors:

\[q(x)=Q x/L\]

Notons \(S=\pi D^2/4\) la surface intérieure de la conduite. On obtient la perte de charge en intégrant la relation de Darcy-Weisbach:

\[\Delta H=\int_{x=0}^{L} a Re^{-0.25} \frac{u^2(x)}{2gD}dx\]

Notons \(\nu\) la viscosité cinématique. On remplace alors \(Re\) par \(u D/\nu\), ce qui donne

\[\Delta H=\int_{x=0}^{L} a u(x)^{-0.25}D^{-0.25}\nu ^{0.25} \frac{u^2(x)}{2gD}dx\]

En réarrangeant, on obtient:

\[\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{u^{1.75}(x)}{2gD^{1.25}}dx\]

Utilisons l'équation du débit pour faire apparaître le débit (\(u(x)=q(x)/S\)):

\[\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{(Qx/(LS))^{1.75}}{2gD^{1.25}}dx\]

puis le diamètre \(D\) :

\(\(\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{(4Qx/(L\pi D^2))^{1.75}}{2gD^{1.25}}dx\)\) On réarrange pour obtenir

\[\Delta H=a \nu ^{0.25} \frac{(4/\pi)^{1.75}Q^{1.75}}{2g D^{4.75}} \int_{x=0}^{L} (x/L)^{1.75}dx\]

En intégrant, on obtient

\[\Delta H=a \nu ^{0.25} \frac{(4/\pi)^{1.75}Q^{1.75}}{2g D^{4.75}}\frac{L}{2.75}\]

\[\Delta H=a \nu ^{0.25} \frac{4^{1.75}}{5.5g \pi^{1.75}}\frac{Q^{1.75}L}{D^{4.75}}\]

Application numérique

Pour une eau à 20°C: \(\nu\simeq 10^{-6}\) m²/s, ce qui donne

\[\Delta H=0.323\ 10^{-3}\frac{Q^{1.75}}{D^{4.75}}L\]

avec \(\Delta H\) en mètres.

Pour une eau à 50°C, \(\nu\simeq 0.556 10^{-6}\) m²/s, ce qui implique que la perte de charge est réduite d'environ 14%, soit

\[\Delta H= 0.28\ 10^{-3}\frac{Q^{1.75}}{D^{4.75}}L\]