Passe à ralentisseurs plans (Denil)

Tous les concepts et formules sont extraits de la référence suivante:

Larinier, M. 2002. “BAFFLE FISHWAYS.” Bulletin Français de La Pêche et de La Pisciculture, no. 364: 83–101. doi:10.1051/kmae/2002109

Caractéristiques géométriques

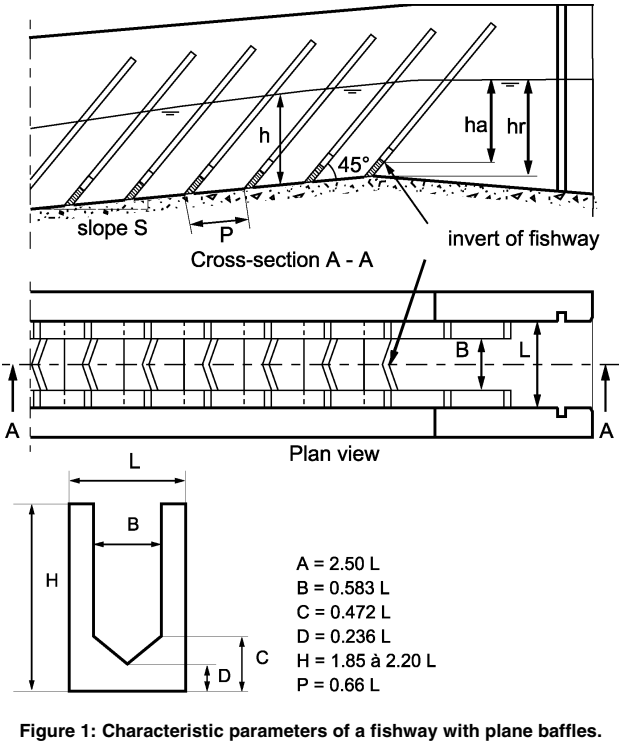
Extrait de Larinier, 2002

Lois hydrauliques issues des abaques

Les expériences effectuées par Larinier, 2002 ont permis d'établir des abaques permettant de relier le débit adimensionnel \(Q^*\) :

\[ Q^* = \dfrac{Q}{\sqrt{g}L^{2,5}} \]

à la charge amont \(ha\) et le niveau d'eau moyen dans la passe \(h\) :

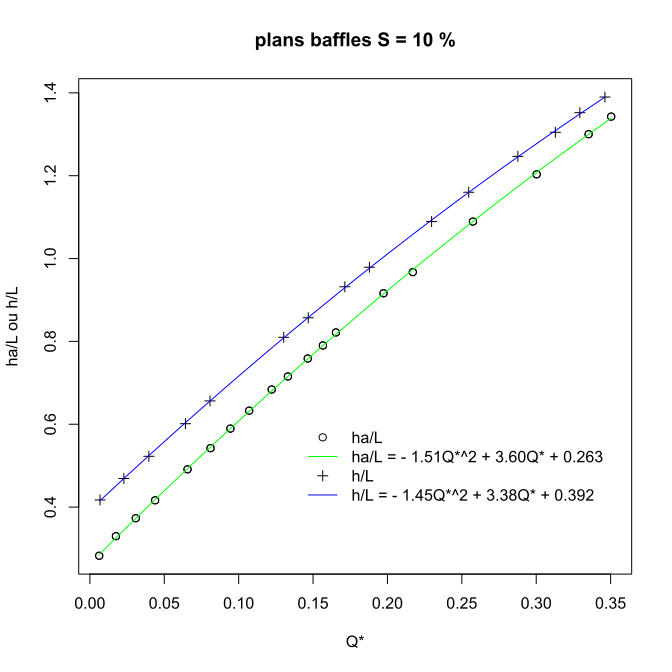
Abaques d'une passe à ralentisseurs plans (Denil) pour une pente de 10% (Extrait de Larinier, 2002)

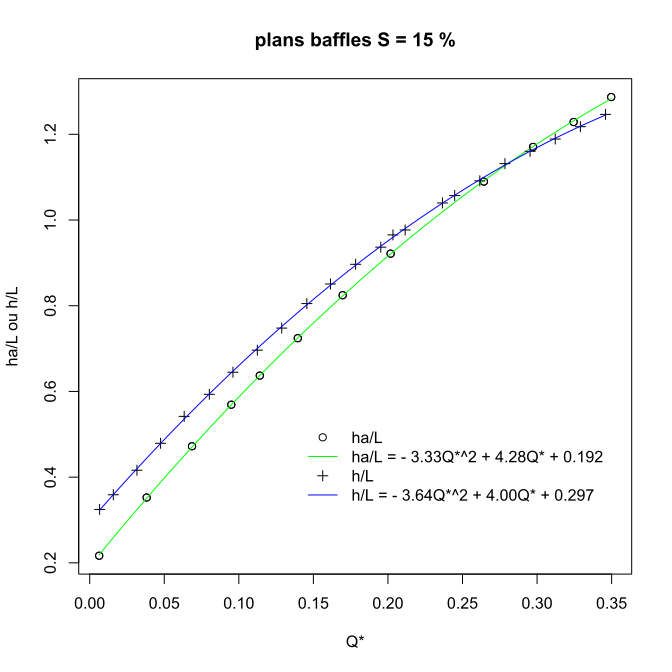
Abaques d'une passe à ralentisseurs plans (Denil) pour une pente de 15% (Extrait de Larinier, 2002)

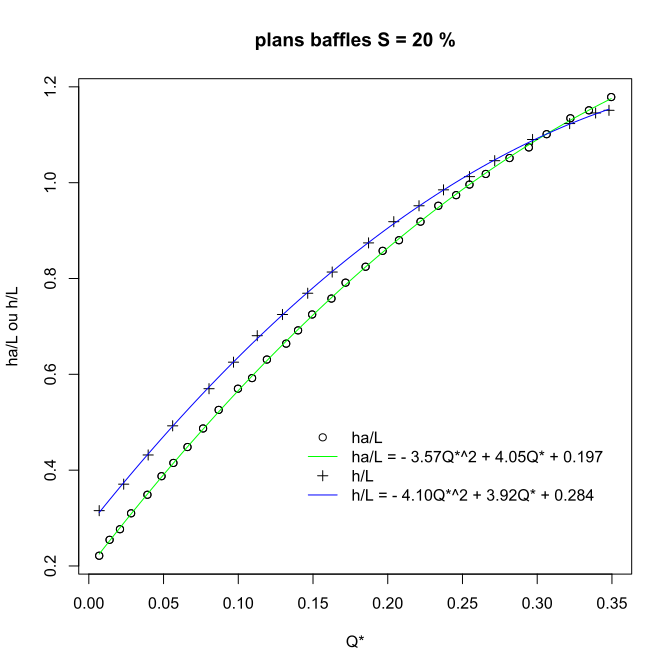
Abaques d'une passe à ralentisseurs plans (Denil) pour une pente de 20% (Extrait de Larinier, 2002)

Pour effectuer les calculs pour toutes les pentes entre 8% et 22%, les coefficients de polynômes des abaques ci-dessus sont eux-mêmes ajustés sous la forme de polynômes dépendant de la pente \(S\).

On a donc :

\[ ha/L = a_2(S) Q^{*2} + a_1(S) Q^* + a_0(S) \]

\[a_2(S) = 315.110S^2 - 115.164S + 6.85371\]

\[a_1(S) = - 184.043S^2 + 59.7073S - 0.530737\]

\[a_0(S) = 15.2115S^2 - 5.22606S + 0.633654\]

Et :

\[ h/L = b_2(S) Q^{*2} + b_1(S) Q^* + b_0 \]

\[b_2(S) = 347.368S^2 - 130.698S + 8.14521\]

\[b_1(S) = - 139.382S^2 + 47.2186S + 0.0547598\]

\[b_0(S) = 16.7218S^2 - 6.09624S + 0.834851\]

Calcul de \(ha\), \(h\) et \(Q\)

On peut ensuite utiliser ces coefficients pour calculer \(ha\), \(h\) et \(Q^*\) :

\[ ha = L \left( a_2 (Q^*)^2 + a_1 Q^* + a_0 \right)\]

\[ h = L \left( b_2 (Q^*)^2 + b_1 Q^* + b_0 \right)\]

En utilisant la fonction inverse positive en fonction de \(ha/L\), on obtient:

\[ Q^* = \dfrac{-a_1 + \sqrt{a_1^2 - 4 a_2 (a_0 - h_a/L)}}{2 a_2}\]

Et on a enfin :

\[ Q = Q^* \sqrt{g} L^{2,5} \]

Les limites de calcul de \(Q^*\), \(ha/L\) et \(h/L\) sont fixées à partir des extrémités des courbes des abaques.

Vitesse débitante

La vitesse débitante \(V\) va correspondre à la vitesse moyenne d'écoulement compte tenu de la section d'écoulement \(A_w\) au droit du ralentisseur :

\[ V = \dfrac{Q}{A_w} \]

pour les passes à ralentisseurs plans en utilisant les notations du schéma ci-dessus, on aura :

\[ A_w = B \times \left( h - \dfrac{C+D}{2} \sin(45°) \right)\]

Ce qui donne avec les proportions standards :

\[ A_w = L \left(0.583 h - 0.146L \right) \]

Cote de radier amont \(Z_{r1}\)

\[ Z_{r1} = Z_{d1} - D \sin(45° + \arctan(S)) \]

Cote d'arase minimale des murs latéraux \(Z_m\)

\[ Z_m = Z_{r1} + - H_{min} \sin(45° + \arctan(S)) \]