Vanne dénoyée

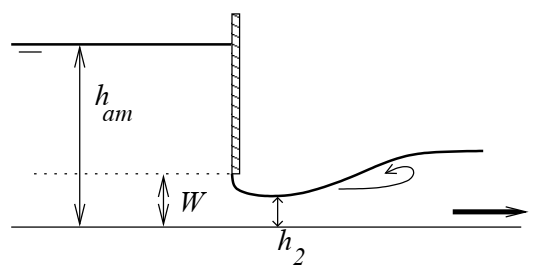
Extrait de Baume, J.-P., Belaud, G., Vion, P.-Y., 2013. Hydraulique pour le génie rural, Formations de Master, Mastère Spécialisé, Ingénieur agronome. UMR G-EAU, Irstea, SupAgro Montpellier.

\(W\) est l'ouverture de la vanne, \(h_{am}\) la hauteur d'eau à l'amont et \(L\) la largeur de la vanne. L'équation de la vanne dénoyée s'obtient à partir de la relation de Bernoulli de conservation de la charge entre l'amont de la vanne et la section contractée.

La hauteur \(h_2\) correspond à la section contractée et est égale à \(C_c W\) où \(C_c\) est le coefficient de contraction. On exprime souvent l'équation de la vanne dénoyée en fonction d'un coefficient de débit sous la forme :

\(Q = C_d L W \sqrt{2g} \sqrt{h_{am}}\)

Ainsi, on a la relation entre \(C_d\) et \(C_c\) :

\(C_d = \frac{C_c}{\sqrt{1 + C_c W / h_{am}}}\)

De nombreuses expériences ont été faites pour évaluer \(C_d\), qui varie peu autour de 0.6. En première approximation, pour \(W / h_{am}\) faible (vanne de fond, cas le plus classique), \(C_d\) est proche de \(C_c\) et peut être pris égal à 0.6.

Les coefficients de débit \(C_d\) sont donnés par des abaques, que l'on trouvera dans des ouvrages spécialisés si besoin. Ils sont de l'ordre de 0.5 à 0.6 pour une vanne verticale, de 0.6 à 0.7 pour une vanne radiale, jusqu'à 0.8 pour une vanne inclinée par rapport à la verticale.