Formule du déversoir triangulaire

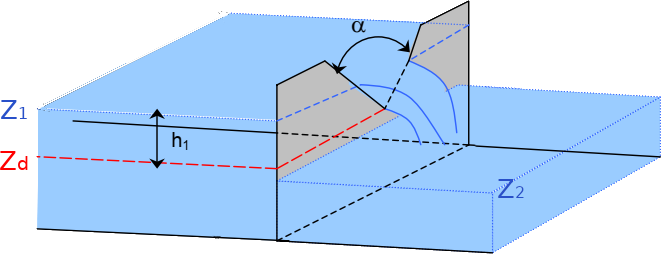
Vue en perspective d'un déversoir triangulaire (d'après CETMEF, 2005¹)

Formule du déversoir dénoyé

\[Q = C_d * \tan \left( \frac{\alpha}{2} \right) \left ( Z_{1} - Z_d \right )^{2.5}\]

Avec:

• \(C_d\) : coefficient de débit
• \(\alpha / 2\) : le demi-angle au sommet du triangle
• \(Z_1\) : cote de l'eau à l'amont du seuil
• \(Z_d\) : cote de déversement de la pointe du triangle

Le coefficient de débit \(C_d\) dépend notamment de l'épaisseur du déversoir:

• Déversoir en mince paroi : \(C_d\) = 1.37
• Déversoir épais sans contraction (arrondi \(r > 0.1 * h1\)) : \(C_d\) = 1.27
• Déversoir à profil triangulaire : (1/2 amont, 1/2 ou 1/5 aval) : \(C_d\) = 1.68 et 1.56

Ennoiement d'un seuil triangulaire mince

Le seuil est noyé dès que \(Z_{2} > Z_{d}\) et le coefficient de réduction de Villemonte est alors appliqué sur le débit calculé en régime dénoyé.

Ennoiement d'un seuil triangulaire épais

L'ennoiement a lieu pour \(h_2 / h_1 > 4 / 5\) avec \(h_1 = Z_1 - Z_d\) et \(h_2 = Z_2 - Z_d\), et avec \(Z_2\) la cote de l'eau à l'aval du seuil.

Le coefficient de réduction proposé par Bos (1989)² est alors appliqué:

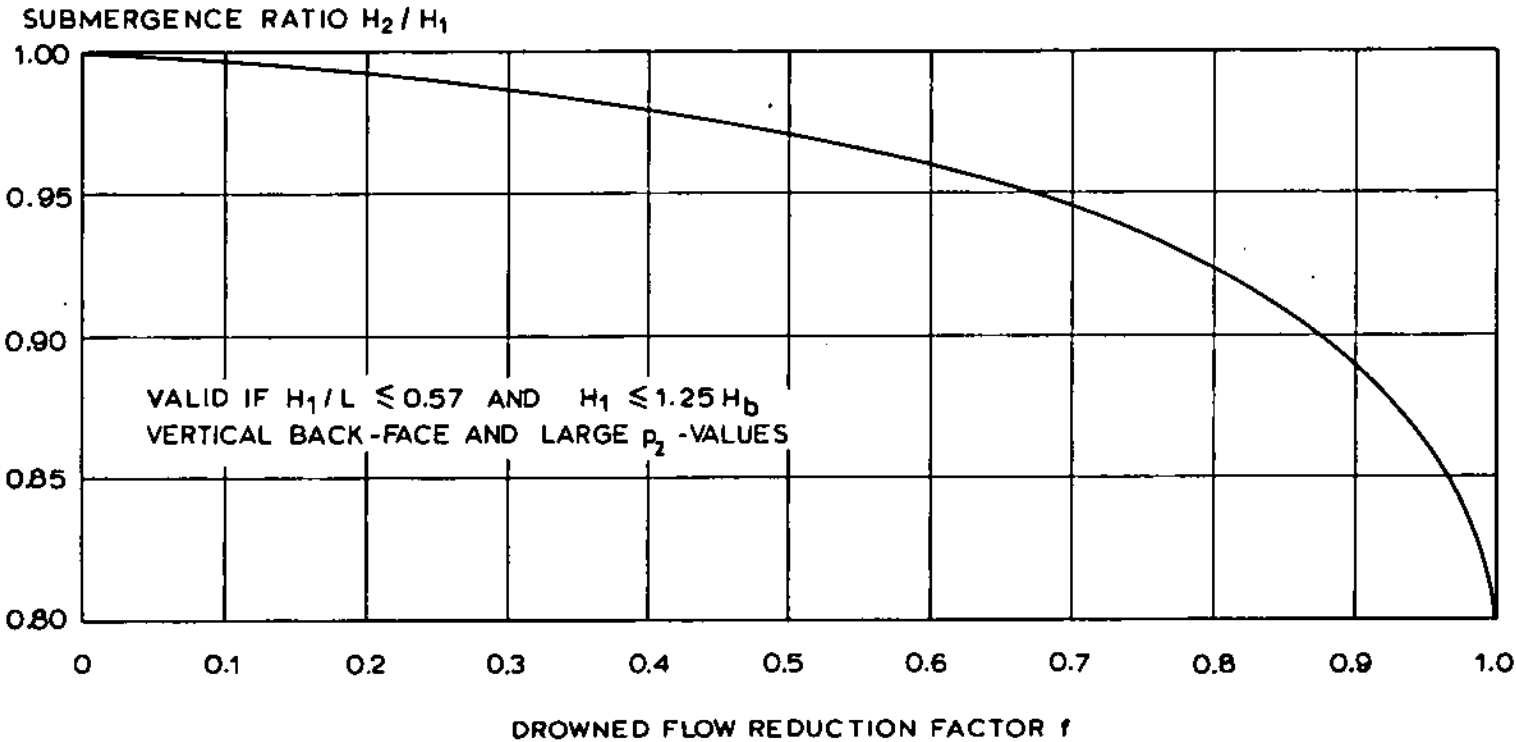
Coefficient d'ennoiement pour un déversoir triangulaire à crête épaisse (extrait de Bos, 1989 ²)

L'abaque est approché par la formule suivante :

\[K_s = sin(3.9629 (1 - h_2 / h_1)^{0.575})\]

---

1. CETMEF, 2005. Notice sur les déversoirs : synthèse des lois d’écoulement au droit des seuils et déversoirs. Centre d’Études Techniques Maritimes Et Fluviales, Compiègne. ↩

2. Bos, M.G., 1989. Discharge measurement structures., 3rd edition. ed, Publication. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands. ↩↩↩