CEM88(V) : Déversoir / Vanne de fond (pelle faible)

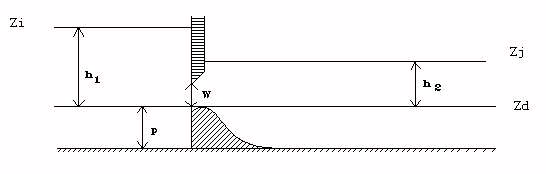
Déversoir - régime dénoyé

\(Q=\mu_f L \sqrt{2g} h_1^{3/2}\)

Déversoir - régime noyé

\(Q=k_F \mu_F L \sqrt{2g} h_1^{3/2}\)

\(k_F\) coefficient de réduction de débit en noyé. Le coefficient de réduction de débit est fonction de \(\frac{h_2}{h_1}\) et de la valeur \({\alpha}\) de ce rapport au moment du passage noyé dénoyé. L’ennoiement est obtenu quand \(\frac{h_2}{h_1} > \alpha\). La loi de variation de \(k_F\) a été ajustée sur les résultats expérimentaux (\(\alpha= 0.75\)).

Posons \(x = \sqrt{1-\frac{h_2}{h_1}}\) :

• Si \(x > 0.2 : k_F = 1 - \left(1 - \frac{x}{\sqrt{1-\alpha}}\right)^\beta\)
• Si \(x \leq 0.2 : k_F = 5x \left(1 - \left(1 - \frac{0.2}{\sqrt{1-\alpha}} \right)^\beta \right)\)

Avec \(\beta = -2\alpha + 2.6\), on calcule un coefficient de débit dénoyé équivalent comme précédemment.

Vanne de fond - régime dénoyé

\(Q = L \sqrt{2g} \left(\mu h_1^{3/2} - \mu_1 (h_1 - W)^{3/2} \right)\)

On constate expérimentalement que le coefficient de débit d’une vanne augmente avec \(\frac{h_1}{W}\). On a ajusté une loi de variation de \(\mu\) de la forme :

\(\mu = \mu_0 - \frac{0.08}{\frac{h_1}{W}}\) avec : \(\mu_0 \simeq 0.4\)

donc \(\mu_1 = \mu_0 - \frac{0.08}{\frac{h_1}{W}-1}\)

Pour assurer la continuité avec la surface libre dénoyé pour \(\frac{h1}{W} = 1\), il faut donc que \(\mu_F = \mu_0 - 0.08\) soit \(\mu_F = 0.32\) pour \(\mu_0 = 0.4\)

Vanne de fond - régime noyé

Régime partiellement noyé

\(Q = L \sqrt{2g} \left[k_F \mu h_1^{3/2} - \mu_1 \left(h_1 - W \right)^{3/2} \right]\)

\(k_F\) étant le même que pour la surface libre.

Le passage noyé-dénoyé a été ajusté sur les résultats expérimentaux, on a une loi du type :

\(\alpha = 1 - 0.14 \frac{h_2}{W}\)

\(0.4 \leq \alpha \leq0.75\)

Pour assurer la continuité avec le fonctionnement à surface libre, il faut donc que le passage noyé-dénoyé à surface libre se fasse pour \(\alpha = 0.75\) au lieu de \(2/3\) dans la formulation déversoir orifice.

Régime totalement noyé

\(Q = L \sqrt{2g} \left(k_F \mu h_1^{3/2} - k_{F1} \mu_1 \left(h_1 - W \right)^{3/2} \right)\)

La formulation de \(k_{F1}\) est la même que celle de \(k_{F}\) en remplaçant \(h_2\) par \(h_2-W\) (et \(h_1\) par \(h_1-W\)) pour le calcul du coefficient \(x\) et de \({\alpha}\) (et donc de \(k_{F1}\)).

Le passage en totalement noyé a lieu pour :

\(h_2 > \alpha_1 h_1 + (1 - \alpha_1) W\)

avec : \(\alpha_1 = 1 - 0.14 \frac{h_2 - W}{W}\)

\((\alpha_1 = \alpha (h_2-W))\)

Le fonctionnement déversoir-vanne est représenté par les équations ci-dessus et la figure 20. Quel que soit le type d’écoulement en charge, on calcule un coefficient de débit dénoyé équivalent correspondant à une formulation classique de la vanne dénoyée :

\(C_F = \frac{Q}{L\sqrt{2g} W \sqrt{h_1}}\)

Le coefficient directeur par défaut pour l’ouvrage est un coefficient \(C_G\) habituellement proche de \(0.6\). On le transforme alors en \(\mu_0 = \frac{2}{3} C_G\), qui permet de calculer \(\mu\) et \(\mu_1\) de l’équation de la vanne dénoyée.

Remarque : il est possible d’obtenir \(C_F \neq C_G\), même en régime dénoyé, du moment que le coefficient de débit augmente avec le rapport \(\frac{h_1}{W}\).

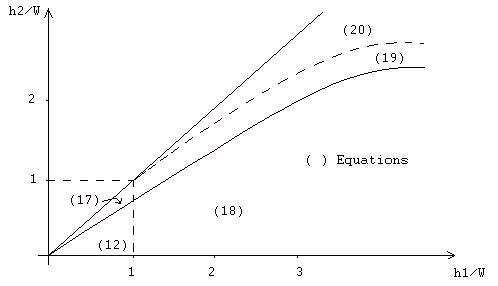
• (12) : Déversoir - dénoyé
• (19) : Orifice - partiellement noyé
• (17) : Déversoir - régime noyé
• (20) : Orifice - totalement noyé
• (18) : Orifice - dénoyé

Figure 20. Déversoir - orifice