Distributor pipe

Analytical relationship for the direct calculation of pressure drops in pipes distributing a flow rate in a homogeneous manner based on the Blasius formula.

Assumptions

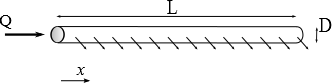
We assume a pipe length \(L\), inner diameter \(D\), with a flow rate at the top \(Q\). We calculate the pressure drop between the two ends of the pipe. In a constant flow section \(q\), the friction coefficient is evaluated with the Blasius formula, valid for moderate Reynolds numbers for smooth walls:

\[\lambda \simeq a Re^{-0.25}\]

Analytical development

We're recording the position from the downstream end of the pipe. The flow rate is supposed to vary linearly with \(x\), and is then written:

\[q(x)=Q x/L\]

Let's note \(S=\pi D^2/4\) the inner surface of the pipe. The pressure drop is obtained by integrating the Darcy-Weisbach relationship:

\[\Delta H=\int_{x=0}^{L} a Re^{-0.25} \frac{u^2(x)}{2gD}dx\]

Note the kinematic viscosity. We then replace \(Re\) with \(u D/\nu\), which gives

\[\Delta H=\int_{x=0}^{L} a u(x)^{-0.25}D^{-0.25}\nu ^{0.25} \frac{u^2(x)}{2gD}dx\]

By rearranging, we get:

\[\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{u^{1.75}(x)}{2gD^{1.25}}dx\]

Let's use the flow equation to show the flow (\(u(x)=q(x)/S\)):

\[\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{(Qx/(LS))^{1.75}}{2gD^{1.25}}dx\]

then the diameter:

\(\(\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{(4Qx/(L\pi D^2))^{1.75}}{2gD^{1.25}}dx\)\) We rearrange to get

\[\Delta H=a \nu ^{0.25} \frac{(4/\pi)^{1.75}Q^{1.75}}{2g D^{4.75}} \int_{x=0}^{L} (x/L)^{1.75}dx\]

By integrating, we obtain

\[\Delta H=a \nu ^{0.25} \frac{(4/\pi)^{1.75}Q^{1.75}}{2g D^{4.75}}\frac{L}{2.75}\]

\[\Delta H=a \nu ^{0.25} \frac{4^{1.75}}{5.5g \pi^{1.75}}{Q^{1.75}L}{D^{4.75}}\]

Digital application

For water at 20°C: \(\nu\simeq 10^{-6}\) m²/s, which gives

\[Delta H=0.323\ 10^{-3}\frac{Q^{1.75}}{D^{4.75}}L\]

with \(\Delta H\) in meters.

For water at 50°C, \(\nu\simeq 0.556 10^{-6}\) m²/s, which means that the pressure drop is reduced by about 14%, or

\[Delta H= 0.28\ 10^{-3}\frac{Q^{1.75}}{D^{4.75}}L\]