Skip to content

Submerged slot formula

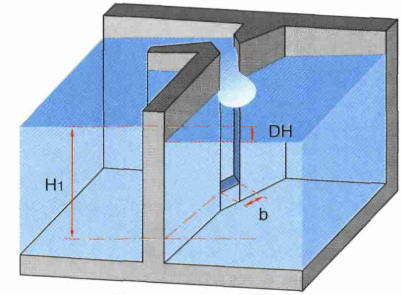
Submerged slot diagram

Excerpt from Larinier, M., Travade, F., Porcher, J.-P., Gosset, C., 1992. Passes à poissons : expertise et conception des ouvrages de franchissement. CSP. (page 94)

Larinier (1992) suggests the following equation:

\[Q = C_d b H_1\sqrt{2g \Delta H}\]

With:

  • b the slot width in m
  • H1 the head on the slot m
  • Cd the discharge coefficient.

Discharge coefficient Cd for the submerged slot formula (vertical slot fish ladder)

The discharge coefficient Cd is an important parameter for the design of vertical slot weirs. This term is integrated in the formula of conveyance of a submerged slot, which connects the transited flow with the fall between basins, the upstream head on the slot and its width.

For single vertical slot weirs, model-reduced studies and numerical simulations have determined average values of discharge coefficients for different configurations, for a typical slot and baffle geometry defined from vertical slot weirs built in France (Figure 1). A different slot and baffle geometry can induce deviations from the average values of the discharge coefficients according to the configurations indicated below.

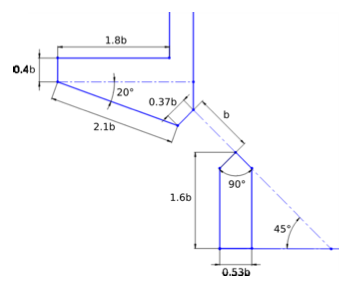
Figure 1

Figure 1: typical slot and baffle geometry from which the discharge coefficient values were determined (Ballu, 2017)

  • Under smooth apron conditions (no bottom roughness) and in the absence of a weir in the slot, Wang et al. (2010) and Ballu et al. (2017) showed that the value of Cd is not significantly influenced by discharge and depends mainly on the slope S (%) and the ratio of the basin width B to the slot width b (B/b).

  • Under smooth invert conditions (no bottom roughness) with the presence of a weir in the slot, under 3 configurations of weir heights hs/b related to slot width b (hs/b = 0.5, 1, and 1.5), Ballu et al. (2015) and Ballu (2017) showed that the value of Cd is not significantly influenced by discharge, and is mainly influenced by slope S, aspect ratio B/b, and weir height hs/b.

  • Under apron conditions with precast bottom roughnesses and in the absence of a weir in the slot, with evenly distributed roughnesses of height hr/b = 2/3 and diameter Ør/b = 1/2, under 2 configurations of densities dr of 10% and 15%, Ballu et al. (2017) and Ballu (2017) showed that the value of Cd is not significantly influenced by discharge, and is mainly influenced by slope S, aspect ratio B/b, and the presence of the bottom roughness dr.

Depending on these different configurations, the average values of the discharge coefficient range from about 0.62 to nearly 0.88 (Figure 2).

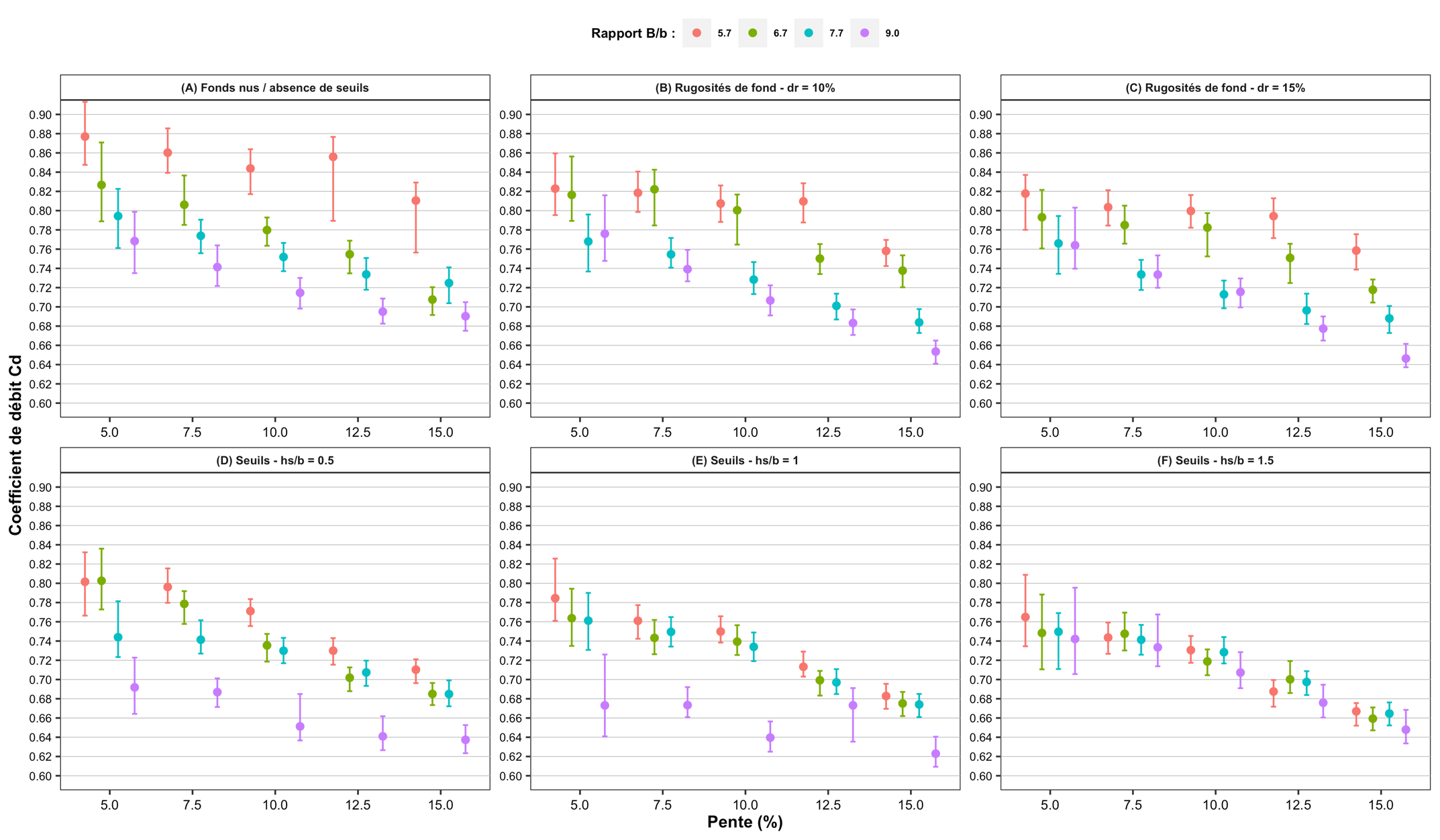
Figure 2

Figure 2: average values and uncertainties (95% confidence intervals, k = 2) of the discharge coefficients according to the slope S and the shape ratio B/b, for different configurations: (A) smooth raft without weir in the slot, (B) bottom roughness dr = 10% without weir in the slot, (C) bottom roughness dr = 15% without weir in the slot, (D) weir in the slot hs/b = 0.5 and smooth raft, (E) weir in the slot hs/b = 1 and smooth raft, (F) weir in the slot hs/b = 1.5 and smooth raft

For passes with double vertical slots, Cd values between 0.75 and 0.80 are commonly used for recently constructed devices with longitudinal slopes between 4% and 5.5%. Studies are under way to clarify the influence of different configurations on discharge coefficients and their corresponding values.

Bibliography:

Ballu A., Pineau G., Calluaud D., David L. (2015). Experimental study of the influence of sills on vertical slot fishway flow. 36th IAHR World Congress, 7p.

Ballu A. (2017). Étude numérique et expérimentale de l’écoulement turbulent au sein des passes à poissons à fentes verticales. Analyse de l’écoulement tridimensionnel et instationnaire. Thèse de l’Université de Poitiers, 223p.

Ballu A., Calluaud D., Pineau G., david L. (2017). Experimental study of the influence of macro-roughnesses on vertical slot fishway flows. La Houille Blanche, 2: 9-14.

Wang R.W., David L., Larinier M. (2010). Contribution of experimental fluid mechanics to the design of vertical slot fish passes. Knowledge and Management of Aquatic Ecosystems, 396(2).