"Fatou" baffle fiwhway

Geometrical characteristics

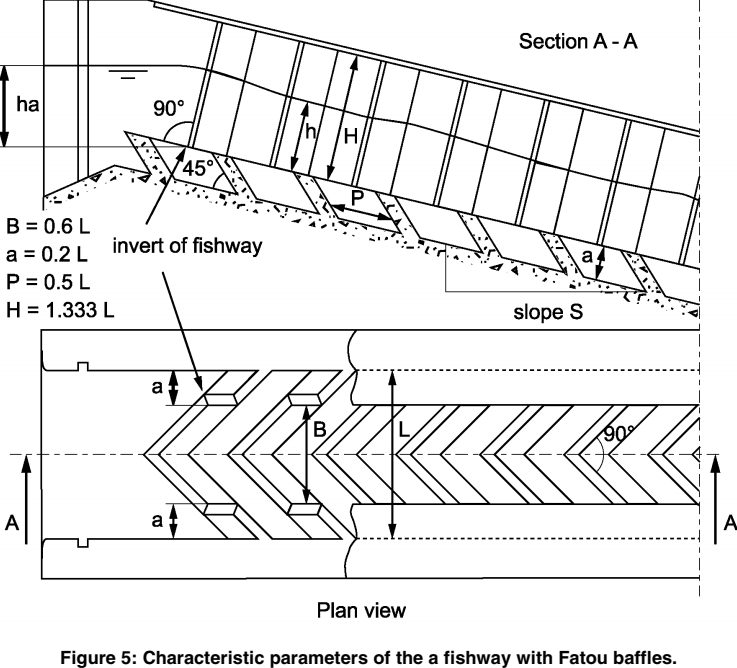
Excerpt from Larinier, 2002¹

Hydraulic laws given by abacuses

Experiments conducted by Larinier, 2002¹ allowed to establish abacuses that link adimensional flow \(Q^*\):

\[ Q^* = \dfrac{Q}{\sqrt{g}L^{2,5}} \]

to upstream head \(ha\) and the average water level in the pass \(h\) :

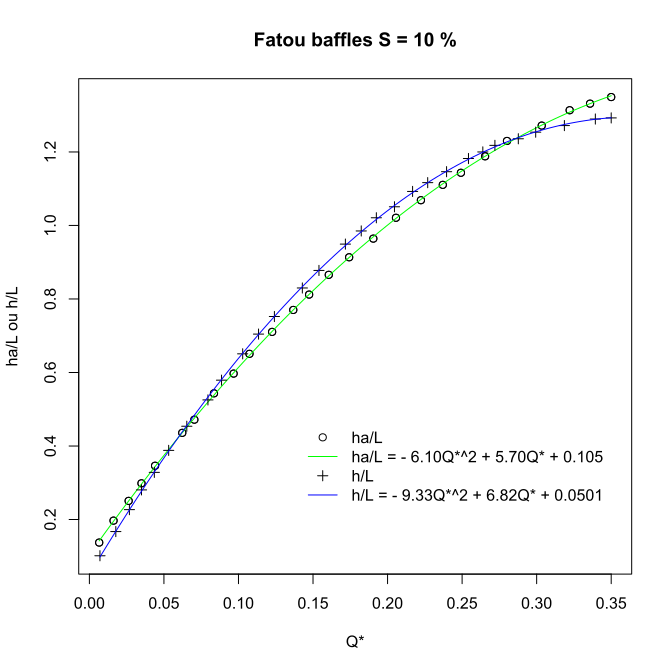
Abacuses of a Fatou baffle fishway for a slope of 10% (Excerpt from Larinier, 2002¹)

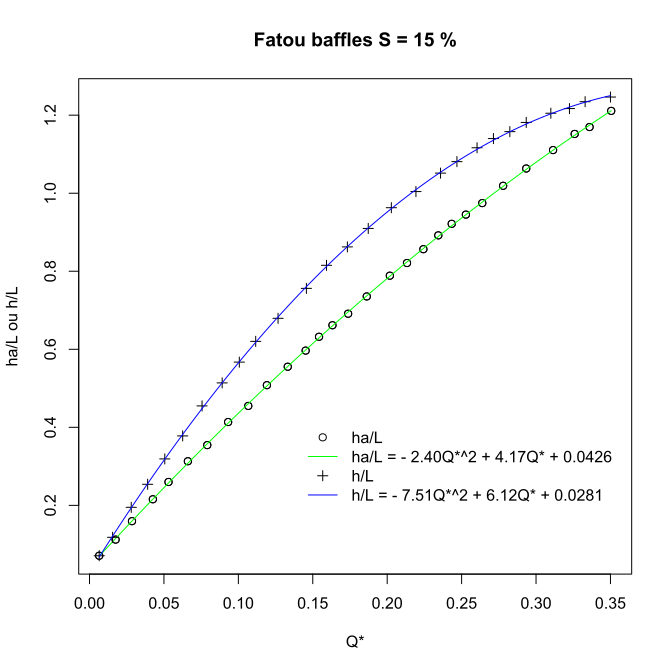
Abacuses of a Fatou baffle fishway for a slope of 15% (Excerpt from Larinier, 2002¹)

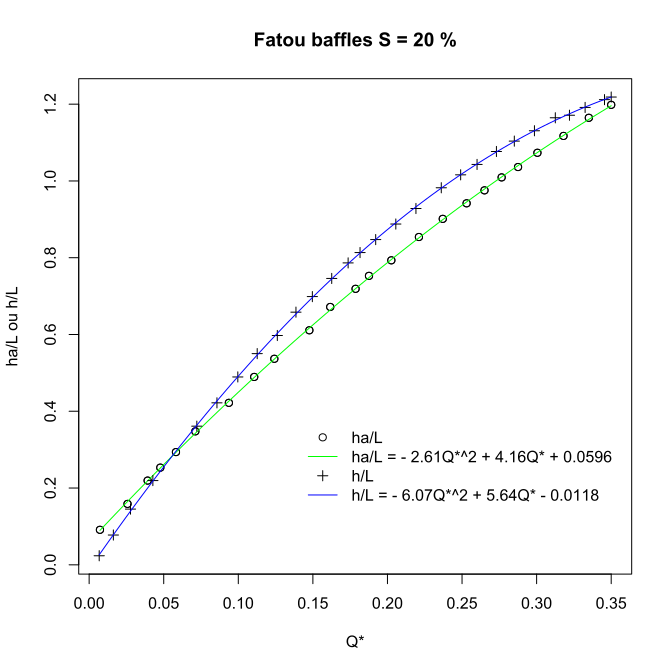
Abacuses of a Fatou baffle fishway for a slope of 20% (Excerpt from Larinier, 2002¹)

To run calculations for all slopes between 8% and 22%, polynomes coefficients of abacuses above are themelves adjusted in the form of slope \(S\) depending polynomes.

We thus have:

\[ ha/L = a_2(S) Q^{*2} + a_1(S) Q^* + a_0(S) \]

\[a_2(S) = - 783.592S^2 + 269.991S - 25.2637\]

\[a_1(S) = 302.623S^2 - 106.203S + 13.2957\]

\[a_0(S) = 15.8096S^2 - 5.19282S + 0.465827\]

And:

\[ h/L = b_2(S) Q^{*2} + b_1(S) Q^* + b_0 \]

\[b_2(S) = - 73.4829S^2 + 54.6733S - 14.0622\]

\[b_1(S) = 42.4113S^2 - 24.4941S + 8.84146\]

\[b_0(S) = - 3.56494S^2 + 0.450262S + 0.0407576\]

Calculation of \(ha\), \(h\) and \(Q\)

We can then use those coefficients to calculate \(ha\), \(h\) and \(Q^*\):

\[ ha = L \left( a_2 (Q^*)^2 + a_1 Q^* + a_0 \right)\]

\[ h = L \left( b_2 (Q^*)^2 + b_1 Q^* + b_0 \right)\]

Using the positive inverse function, depending on \(ha/L\), we get:

\[ Q^* = \dfrac{-a_1 + \sqrt{a_1^2 - 4 a_2 (a_0 - h_a/L)}}{2 a_2}\]

And we finally have:

\[ Q = Q^* \sqrt{g} L^{2,5} \]

Calculation limitations of \(Q^*\), \(ha/L\) and \(h/L\) are determined based on the extremities of the abacuses curves.

Flow velocity

Flow velocity \(V\) corresponds to the minimum flow speed given the flow section \(A_w\) at the perpendicular of the baffle :

\[ V = \dfrac{Q}{A_w} \]

for Fatou baffle fishways using the notation of the schema above, we have:

\[ A_w = B \times h \]

Which gives with standard proportions:

\[ A_w = 0.6hL \]

Upstream apron elevation \(Z_{r1}\)

\[ Z_{r1} = Z_{d1} + \frac{0.3 S - 0.2}{\sqrt{1 + S^2}} \]

Minimal rake height of upstream side walls \(Z_m\)

\[ Z_m = Z_{r1} + \frac{4 L}{3 \sqrt{1 + S^2}} \]

---

1. Larinier, M. 2002. “BAFFLE FISHWAYS.” Bulletin Français de La Pêche et de La Pisciculture, no. 364: 83–101. doi:10.1051/kmae/2002109. ↩↩↩↩↩